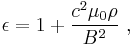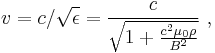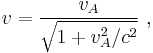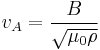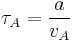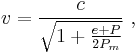Alfvén wave
An Alfvén wave, named after Hannes Alfvén, is a type of magnetohydrodynamic wave.[1]
Contents |
Definition
An Alfvén wave in a plasma is a low-frequency (compared to the ion cyclotron frequency) travelling oscillation of the ions and the magnetic field. The ion mass density provides the inertia and the magnetic field line tension provides the restoring force.
The wave propagates in the direction of the magnetic field, although waves exist at oblique incidence and smoothly change into the magnetosonic wave when the propagation is perpendicular to the magnetic field.
The motion of the ions and the perturbation of the magnetic field are in the same direction and transverse to the direction of propagation. The wave is dispersionless.
Alfvén velocity
The low-frequency permittivity 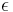 of a magnetized plasma is given by
of a magnetized plasma is given by
where 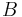 is the magnetic field strength,
is the magnetic field strength, 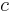 is the speed of light,
is the speed of light, 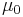 is the permeability of the vacuum, and
is the permeability of the vacuum, and 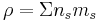 is the total mass density of the charged plasma particles. Here,
is the total mass density of the charged plasma particles. Here, 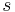 goes over all plasma species, both electrons and (few types of) ions.
goes over all plasma species, both electrons and (few types of) ions.
Therefore, the velocity of an electromagnetic wave in such a medium is
or
where
is the Alfvén velocity. If  , then
, then 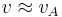 . On the other hand, when
. On the other hand, when 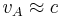 , then
, then 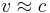 . That is, at high field or low density, the velocity of the Alfvén wave approaches the speed of light, and the Alfvén wave becomes an ordinary electromagnetic wave.
. That is, at high field or low density, the velocity of the Alfvén wave approaches the speed of light, and the Alfvén wave becomes an ordinary electromagnetic wave.
Neglecting the contribution of the electrons to the mass density and assuming that there is a single ion species, we get
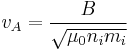 in SI
in SI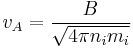 in CGS
in CGS
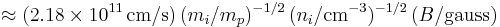
where 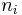 is the ion number density and
is the ion number density and 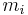 is the ion mass.
is the ion mass.
Alfvén time
In plasma physics, the Alfvén time 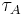 is an important timescale for wave phenomena. It is related to the Alfvén velocity by:
is an important timescale for wave phenomena. It is related to the Alfvén velocity by:
where  denotes the characteristic scale of the system, for example
denotes the characteristic scale of the system, for example  is the minor radius of the torus in a tokamak.
is the minor radius of the torus in a tokamak.
Relativistic case
The general Alfvén wave velocity is defined by Gedalin (1993):[2]
where
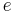 is the total energy density of plasma particles,
is the total energy density of plasma particles, 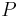 is the total plasma pressure, and
is the total plasma pressure, and 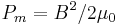 is the magnetic field pressure. In the non-relativistic limit
is the magnetic field pressure. In the non-relativistic limit 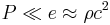 , and we immediately get the expression from the previous section.
, and we immediately get the expression from the previous section.
History
How this phenomenon became understood
- 1942: Alfvén suggests the existence of electromagnetic-hydromagnetic waves in a paper published in Nature.
- 1949: Laboratory experiments by S. Lundquist produce such waves in magnetized mercury, with a velocity that approximated Alfvén's formula.
- 1949: Enrico Fermi uses Alfvén waves in his theory of cosmic rays. According to Alex Dessler in a 1970 Science journal article, Fermi had heard a lecture at the University of Chicago, Fermi nodded his head exclaiming "of course" and the next day, the physics world said "of course".
- 1950: Alfvén publishes the first edition of his book, Cosmical Electrodynamics, detailing hydromagnetic waves, and discussing their application to both laboratory and space plasmas.
- 1952: Additional confirmation appears in experiments by Winston Bostick and Morton Levine with ionized helium
- 1954: Bo Lehnert produces Alfvén waves in liquid sodium
- 1958: Eugene Parker suggests hydromagnetic waves in the interstellar medium
- 1958: Berthold, Harris, and Hope detect Alfvén waves in the ionosphere after the Argus nuclear test, generated by the explosion, and traveling at speeds predicted by Alfvén formula.
- 1958: Eugene Parker suggests hydromagnetic waves in the Solar corona extending into the Solar wind.
- 1959: D. F. Jephcott produces Alfvén waves in a gas discharge
- 1959: C. H. Kelley and J. Yenser produce Alfvén waves in the ambient atmosphere.
- 1960: Coleman, et al., report the measurement of Alfvén waves by the magnetometer aboard the Pioneer and Explorer satellites
- 1960: Sugiura suggests evidence of hydromagnetic waves in the Earth's magnetic field
- 1961: Normal Alfvén modes and resonances in liquid sodium are studied by Jameson
- 1966: R.O.Motz generates and observes Alfven waves in mercury
- 1970 Hannes Alfvén wins the 1970 Nobel Prize in physics for "fundamental work and discoveries in magneto-hydrodynamics with fruitful applications in different parts of plasma physics"
- 1973: Eugene Parker suggests hydromagnetic waves in the intergalactic medium
- 1974: Hollweg suggests the existence of hydromagnetic waves in interplanetary space
- 1974: Ip and Mendis suggests the existence of hydromagnetic waves in the coma of Comet Kohoutek.
- 1999: Aschwanden, et al. and Nakariakov, et al. report the detection of damped transverse oscillations of solar coronal loops observed with the EUV imager on board the Transition Region And Coronal Explorer (TRACE), interpreted as standing kink (or "Alfvénic") oscillations of the loops.
- 2007: Tomczyk, et al., report the detection of Alfvénic waves in images of the solar corona with the Coronal Multi-Channel Polarimeter (CoMP) instrument at the National Solar Observatory, New Mexico. These waves were interpreted as propagating kink waves by Van Doorsselaere et al. (2008)
- 2007: Alfvén wave discoveries appear in articles by Jonathan Cirtain and colleagues, Takenori J. Okamoto and colleagues, and Bart De Pontieu and colleagues. De Pontieu’s team also shows that the energy associated with the waves is sufficient to heat the corona and accelerate the solar wind. These results appear in a special collection of 10 articles, by scientists in Japan, Europe and the United States, in the 7 December issue of the journal Science. It was demonstrated that those waves should be interpreted in terms of kink waves of coronal plasma structures by Van Doorsselaere, et al. (2008); Ofman and Wang (2008); and Vasheghani Farahani, et al. (2009).
- 2011: Experimental evidence of Alfvén wave propagation in a Gallium alloy[3]
See also
- Electrohydrodynamics
- Plasma stability
- Shocks and discontinuities (magnetohydrodynamics)
- Computational magnetohydrodynamics
- Ferrofluid
- MHD generator
- MHD sensor
- Magnetic flow meter
- Magnetohydrodynamic turbulence
- Molten salt
- Electromagnetic pump
- List of plasma (physics) articles
References
- ^ Iwai, K; Shinya, K,; Takashi, K. and Moreau, R. (2003) "Pressure change accompanying Alfvén waves in a liquid metal" Magnetohydrodynamics 39(3): pp. 245-250, page 245
- ^ Gedalin, M. (1993), "Linear waves in relativistic anisotropic magnetohydrodynamics", Physical Review E 47 (6): 4354–4357, Bibcode 1993PhRvE..47.4354G, doi:10.1103/PhysRevE.47.4354
- ^ doi:10.1063/1.3633090
This DOI appears to be broken. It may be incorrect, in which case correcting it will allow the citation to be automatically completed. Or it may not be functional, in which case you can complete the citation details by hand.
Further reading
- Alfvén, H. (1942), "Existence of electromagnetic-hydrodynamic waves", Nature 150 (3805): 405–406, Bibcode 1942Natur.150..405A, doi:10.1038/150405d0
- ——— (1981), Cosmic Plasma, Holland: Reidel, ISBN 9027711518
- Aschwanden, M. J.; Fletcher, L.; Schrijver, C. J.; Alexander, D. (1999), "Coronal Loop Oscillations Observed with the Transition Region and Coronal Explorer", The Astrophysical Journal 520 (2): 880–894, Bibcode 1999ApJ...520..880A, doi:10.1086/307502
- Berthold, W. K.; Harris, A. K.; Hope, H. J. (1960), "World-Wide Effects of Hydromagnetic Waves Due to Argus", Journal of Geophysical Research 65 (8): 2233–2239, Bibcode 1960JGR....65.2233B, doi:10.1029/JZ065i008p02233
- Bostick, Winston H.; Levine, Morton A. (1952), "Experimental Demonstration in the Laboratory of the Existence of Magneto-Hydrodynamic Waves in Ionized Helium", Physical Review 87 (4): 671, Bibcode 1952PhRv...87..671B, doi:10.1103/PhysRev.87.671
- Coleman, P. J., Jr.; Sonett, C. P.; Judge, D. L.; Smith, E. J. (1960), "Some Preliminary Results of the Pioneer V Magnetometer Experiment", Journal of Geophysical Research 65 (6): 1856–1857, Bibcode 1960JGR....65.1856C, doi:10.1029/JZ065i006p01856
- Cramer, N. F.; Vladimirov, S. V. (1997), "Alfvén Waves in Dusty Interstellar Clouds", Publications of the Astronomical Society of Australia 14 (2): 170–178, Bibcode 1997PASA...14..170C, http://www.atnf.csiro.au/pasa/14_2/cramer/paper/
- Dessler, A. J. (1970), "Swedish iconoclast recognized after many years of rejection and obscurity", Science 170 (3958): 604–606, Bibcode 1970Sci...170..604D, doi:10.1126/science.170.3958.604
- Falceta-Gonçalves, D.; Jatenco-Pereira, V. (2002), "The Effects of Alfvén Waves and Radiation Pressure in Dust Winds of Late-Type Stars", Astrophysical Journal 576 (2): 976–981, arXiv:astro-ph/0207342, Bibcode 2002ApJ...576..976F, doi:10.1086/341794
- Fermi, E. (1949), "On the Origin of the Cosmic Radiation", Physical Review 75 (8): 1169–1174, Bibcode 1949PhRv...75.1169F, doi:10.1103/PhysRev.75.1169
- Hollweg, J. V. (1974), "Hydromagnetic waves in interplanetary space", Astronomical Society of the Pacific, Publications 86 (Oct. 1974): 561–594, Bibcode 1974PASP...86..561H, doi:10.1086/129646
- Ip, W.-H.; Mendis, D. A. (1975), "The cometary magnetic field and its associated electric currents", Icarus 26 (4): 457–461, Bibcode 1975Icar...26..457I, doi:10.1016/0019-1035(75)90115-3
- Jephcott, D. F. (1959), "Alfvén waves in a gas discharge", Nature 183 (4676): 1652–1654, Bibcode 1959Natur.183.1652J, doi:10.1038/1831652a0
- Lehnert, Bo (1954), "Magneto-Hydrodynamic Waves in Liquid Sodium", Physical Review 94 (4): 815–824, Bibcode 1954PhRv...94..815L, doi:10.1103/PhysRev.94.815
- Lundquist, S. (1949), "Experimental Investigations of Magneto-Hydrodynamic Waves", Physical Review 76 (12): 1805–1809, Bibcode 1949PhRv...76.1805L, doi:10.1103/PhysRev.76.1805
- Mancuso, S.; Spangler, S. R. (1999), "Coronal Faraday Rotation Observations: Measurements and Limits on Plasma Inhomogeneities", The Astrophysical Journal 525 (1): 195–208, Bibcode 1999ApJ...525..195M, doi:10.1086/307896
- Motz, R. O. (1966), "Alfven Wave Generation in a Spherical System", Physics of Fluids 9 (2): 411–412, Bibcode 1966PhFl....9..411M, doi:10.1063/1.1761687
- Nakariakov, V. M.; Ofman, L.; Deluca, E. E.; Roberts, B.; Davila, J. M. (1999), "TRACE observation of damped coronal loop oscillations: Implications for coronal heating", Science 285 (5429): 862–864, Bibcode 1999Sci...285..862N, doi:10.1126/science.285.5429.862, PMID 10436148
- Ofman, L.; Wang, T. J. (2008), "Hinode observations of transverse waves with flows in coronal loops", Astronomy and Astrophysics 482 (2): L9-L12, Bibcode 2008A&A...482L...9O, doi:10.1051/0004-6361:20079340
- Otani, N. F. (1988a), "The Alfvén ion-cyclotron instability, simulation theory and techniques", Journal of Computational Physics 78 (2): 251–277, Bibcode 1988JCoPh..78..251O, doi:10.1016/0021-9991(88)90049-6
- ——— (1988b), "Application of Nonlinear Dynamical Invariants in a Single Electromagnetic Wave to the Study of the Alfvén-Ion-Cyclotron Instability", Physics of Fluids 31 (6): 1456–1464, Bibcode 1988PhFl...31.1456O, doi:10.1063/1.866736
- Parker, E. N. (1955), "Hydromagnetic Waves and the Acceleration of Cosmic Rays", Physical Review 99 (1): 241–253, Bibcode 1955PhRv...99..241P, doi:10.1103/PhysRev.99.241
- ——— (1958), "Suprathermal Particle Generation in the Solar Corona", Astrophysical Journal 128: 677, Bibcode 1958ApJ...128..677P, doi:10.1086/146580
- ——— (1973), "Extragalactic Cosmic Rays and the Galactic Magnetic Field", Astrophysics and Space Science 24 (1): 279–288, Bibcode 1973Ap&SS..24..279P, doi:10.1007/BF00648691
- Silberstein, M.; Otani, N. F. (1994), "Computer simulation of Alfvén waves and double layers along auroral magnetic field lines", Journal of Geophysical Research 99 (A4): 6351–6365, Bibcode 1994JGR....99.6351S, doi:10.1029/93JA02963, http://otani.vet.cornell.edu/papers/silberstein_otani_1994.pdf
- Sugiura, Masahisa (1961), "Some Evidence of Hydromagnetic Waves in the Earth's Magnetic Field", Physical Review Letters 6 (6): 255–257, Bibcode 1961PhRvL...6..255S, doi:10.1103/PhysRevLett.6.255
- Tomczyk, S.; McIntosh, S. W.; Keil, S. L.; Judge, P. G.; Schad, T.; Seeley, D. H.; Edmondson, J. (2007), "Waves in the Solar Corona", Science 317 (5842): 1192–1196, Bibcode 2007Sci...317.1192T, doi:10.1126/science.1143304
- Van Doorsselaere, T.; Nakariakov, V. M.; Verwichte, E. (2008), "Detection of Waves in the Solar Corona: Kink or Alfvén?", The Astrophysical Journal 676 (1): L73-L75, Bibcode 2008ApJ...676L..73V, doi:10.1086/587029
- Vasheghani Farahani, S.; Van Doorsselaere, T.; Verwichte, E.; Nakariakov, V. M. (2009), "Propagating transverse waves in soft X-ray coronal jets", Astronomy and Astrophysics 498 (2): L29-L32, Bibcode 2009A&A...498L..29V, doi:10.1051/0004-6361/200911840